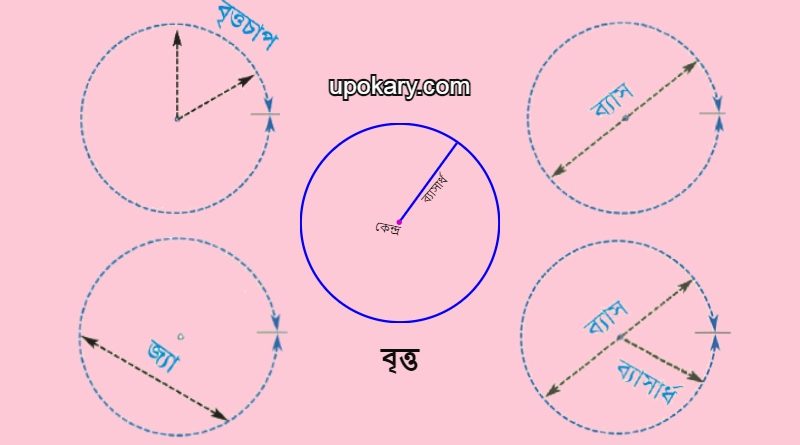
বৃত্ত কাকে বলে? বৃত্তের বিভিন্ন অংশের পরিচয়।

বৃত্তের কেন্দ্র :

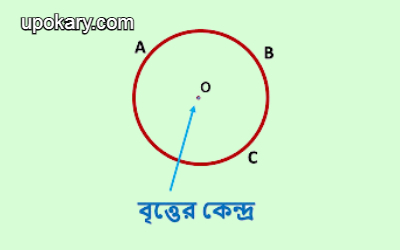
যে নির্দিষ্ট বিন্দু থেকে বৃত্তের পরিধির উপর সকল বিন্দুর দুরত্ব সমান, ঐ নির্দিষ্ট বিন্দুকে বৃত্তের কেন্দ্র বলে। একটি বৃত্তের কেবল একটি মাত্র কেন্দ্র থাকে। তাই বৃত্তের কেন্দ্র একটি অনন্য বিন্দু।

একাধিক বৃত্তের কেন্দ্র একটি হতে পারে। অর্থাৎ, একটি কেন্দ্র দিয়ে একাধিক বৃত্ত অংকন করা যায়। কিন্তু একটি বৃত্তের একাধিক কেন্দ্র থাকতে পারে না। বৃত্তের ব্যাসার্ধ বৃত্তের কেন্দ্রগামী একটি রেখাংশ। আবার, বৃত্তের ব্যাসও বৃত্তের কেন্দ্রগামী একটি রেখাংশ।

বৃত্তচাপ :

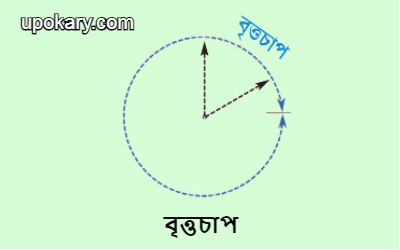
জ্যা দ্বারা বিভক্ত বৃত্তের প্রত্যেক অংশকে বৃত্তচাপ বলে। অথবা, বৃত্তের পরিধিস্থ যেকোনাে দুইটি বিন্দুর দূরত্বকে বৃত্তচাপ বলে। এক কথায় বৃত্তের পরিধির যেকোনাে অংশকে বৃত্তচাপ বলে।

বৃত্তের জ্যা :

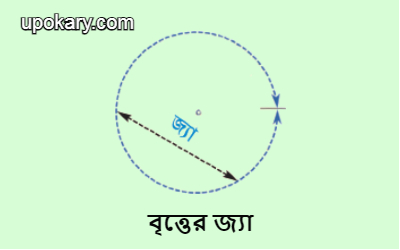
কোনো বৃত্তের বক্ররেখার যেকোনো দুটি বিন্দু কে কোনো সরলরেখা দ্বারা যুক্ত করা হলে যে রেখাংশ টি পাওয়া যায় তাকে জ্যা বলা হয়। অথবা, বৃত্তচাপের শেষ প্রান্তের দুটি বিন্দুর সংযোজক রেখাংশকে জ্যা বলে।

বৃত্তের ব্যাস :

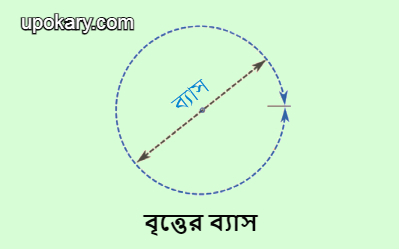
বৃত্তের কেন্দ্র দিয়ে অতিক্রমকারী রেখাংশের প্রান্তবিন্দুদ্বয় বৃত্তের পরিধির উপর অবস্থিত হলে, ঐ রেখাংশকে বৃত্তের ব্যাস বলে। বৃত্তের ব্যাস বৃত্তের ব্যাসার্ধর দ্বিগুণ। বৃত্তের কেন্দ্র বৃত্তের ব্যাসের মধ্যবিন্দু।

আবার বৃত্তের ব্যাস বৃত্তের একটি জ্যা বটে। তবে এটি একটি বিশেষ জ্যা। বৃত্তের ব্যাস বা এই বিশেষ জ্যা বৃত্তের কেন্দ্র দিয়ে যায়। বৃত্তের ব্যাসই বৃহত্তম জ্যা।

বৃত্তের ব্যাসার্ধ :

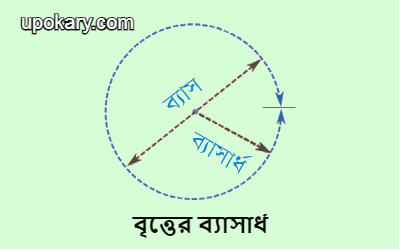
বৃত্তের কেন্দ্র থেকে পরিধির উপর যে কোন বিন্দুর দুরত্বকে বৃত্তের ব্যাসার্ধ বলে। অন্যভাবে বললে, বৃত্তের কেন্দ্র থেকে পরিধির উপর যে কোন বিন্দুর দূরত্বকে বৃত্তের ব্যাসার্ধ বলে। অর্থাৎ, বৃত্তের কেন্দ্র ও পরিধির উপর যে কোন বিন্দুর সংযোজক রেখাংশ হলো বৃত্তের ব্যাসার্ধ। একটি বৃত্তে অসংখ্য ব্যাসার্ধ আঁকা যায়।

বৃত্তের পরিধি :

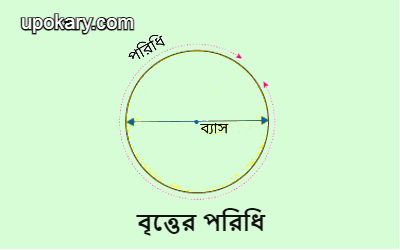
একটি বৃত্তের কেন্দ্র হতে সমান দূরত্ব বজায় রেখে কোন বিন্দুর চলার পথের দৈর্ঘ্যকে বৃত্তের পরিধি বলে। অথবা, বৃত্তের সীমান্ত বরাবর দৈর্ঘ্যকে বৃত্তের পরিধি বলে। অতএব বৃত্তের পরিধি হলো বৃত্তের পরিসীমা।

বৃত্তস্থ কোণ :

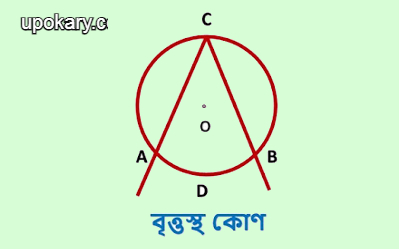
একটি কোণের শীর্ষবিন্দু কোনো বৃত্তের একটি বিন্দু হলে এবং কোণটির প্রত্যেক বাহুতে শীর্ষবিন্দু ছাড়াও বৃত্তের একটি বিন্দু থাকলে কোণটিকে একটি বৃত্তস্থ কোণ বলে।

কেন্দ্রস্থ কোণ :

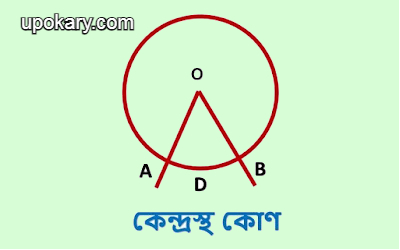
একটি কোণের শীর্ষবিন্দু কোন বৃত্তের কেন্দ্রে অবস্থিত হলে কোণটিকে ঐ বৃত্তের একটি কেন্দ্রস্থ কোণ বলা হয়। অথবা, কোন বৃত্তচাপের প্রান্তদ্বয় হতে সৃষ্ট দুটি সরলরেখা বৃত্তের কেন্দ্র মিলিত হলে যে কোণ উৎপন্ন করে তাকে কেন্দ্রস্থ কোণ বলে।